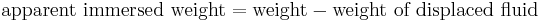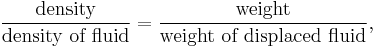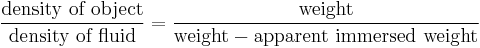Archimedes' principle

Archimedes' principle relates buoyancy to displacement. It is named after its discoverer, Archimedes of Syracuse.[1]

Contents

Principle

Archimedes' treatise On floating bodies, proposition 5, states that

Any floating object displaces its own weight of fluid.

—Archimedes of Syracuse[2]

For more general objects, floating and sunken, and in gasses as well as liquids (i.e. a fluid), Archimedes' principle may be stated thus in terms of forces:

Any object, wholly or partially immersed in a fluid, is buoyed up by a force equal to the weight of the fluid displaced by the object.

— Archimedes of Syracuse

with the clarifications that for a sunken object the volume of displaced fluid is the volume of the object, and for a floating object on a liquid, the weight of the displaced liquid is the weight of the object.

In short, buoyancy = weight of displaced fluid.

Refinements

Archimedes' principle does not consider the surface tension (capillarity) acting on the body.[3]

Formula

The weight of the displaced fluid is directly proportional to the volume of the displaced fluid (if the surrounding fluid is of uniform density). In simple terms, the principle states that the buoyant force on an object is going to be equal to the weight of the fluid displaced by the object, or the density of the fluid multiplied by the submerged volume times the gravitational constant, g. Thus, among completely submerged objects with equal masses, objects with greater volume have greater buoyancy.

Suppose a rock's weight is measured as 10 newtons when suspended by a string in a vacuum with gravity acting upon it. Suppose that when the rock is lowered into water, it displaces water of weight 3 newtons. The force it then exerts on the string from which it hangs would be 10 newtons minus the 3 newtons of buoyant force: 10 − 3 = 7 newtons. Buoyancy reduces the apparent weight of objects that have sunk completely to the sea floor. It is generally easier to lift an object up through the water than it is to pull it out of the water.

Assuming Archimedes' principle to be reformulated as follows,

\text{apparent immersed weight} = \text{weight} - \text{weight of displaced fluid}\,

then inserted into the quotient of weights, which has been expanded by the mutual volume

\frac { \text{density}} { \text{density of fluid} } = \frac { \text{weight}} { \text{weight of displaced fluid} }, \,

yields the formula below. The density of the immersed object relative to the density of the fluid can easily be calculated without measuring any volumes:

\frac { \text {density of object}} { \text{density of fluid} } = \frac { \text{weight}} { \text{weight} - \text{apparent immersed weight}}\,

(This formula is used for example in describing the measuring principle of a dasymeter and of hydrostatic weighing.)

Example: If you drop wood into water buoyancy will keep it afloat.

Example: A helium balloon in a moving car. In increasing speed or driving a curve, the air moves in the opposite direction of the car's acceleration. The balloon however, is pushed due to buoyancy "out of the way" by the air, and will actually drift in the same direction as the car's acceleration.

See also

References

  1. ^ Acott, Chris (1999). "The diving "Law-ers": A brief resume of their lives.". South Pacific Underwater Medicine Society journal 29 (1). ISSN 0813-1988. OCLC 16986801. http://archive.rubicon-foundation.org/5990. Retrieved 2009-06-13. 
  2. ^ "The Works of Archimedes". p. 257. http://www.archive.org/stream/worksofarchimede00arch#page/256/mode/2up. Retrieved 11 March 2010. "Any solid lighter than a fluid will, if placed in the fluid, be so far immersed that the weight of the solid will be equal to the weight of the fluid displaced." 
  3. ^ "Floater clustering in a standing wave: Capillarity effects drive hydrophilic or hydrophobic particles to congregate at specific points on a wave" (PDF). 2005-06-23. http://www.weizmann.ac.il/home/fnfal/papers/Natfloat.pdf.